Два новых закона сохранения энергии в задаче двух тел.
Результаты численных расчетов для n-законов сохранения энергии для n-тел.
Виктор Воронков. vv-2000@list.ru сентябрь-ноябрь 2013 г.
Посмотреть фильм.
Считается, что для системы тел, взаимодействующих с помощью консервативных сил, существует только один закон сохранения суммарной (полной) энергии всех тел.
Однако и для общепознавательных целей , равно как для практических целей численного интегрирования системы уравнений движения, большой интерес представляют законы сохранения энергии для каждого из взаимодействующих тел. В последнем случае наличие формулы, которая позволит проконтролировать погрешность расчета для каждого тела в задаче многих тел, независимо от числа шагов интегрирования и выбранной численной схемы, представляет большую ценность.
Поэтому здесь я привожу свой вывод двух законов сохранения энергии в задаче двух тел и привожу результаты расчета для многих тел, которые показывают, что существование n законов сохранения энергии для системы из n-тел возможно.
Законы сохранения энергии для каждого тела в задаче двух тел в системе координат центра масс имеют вид:
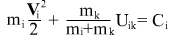
здесь i и k - номера тел: i=1,2 k=2,1
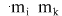 - массы тел - массы тел
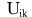 - потенциал тела k в точке нахождения тела i - потенциал тела k в точке нахождения тела i
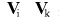 - скорости тел i и k в момент времени t - скорости тел i и k в момент времени t
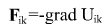 - консервативная сила, действующая на тело i со стороны тела k - консервативная сила, действующая на тело i со стороны тела k
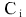 - константа (независящая от времени величина) - константа (независящая от времени величина)
Вы можете протестировать формулу для сохранение энергий с помощью программы TWO-LAW , которая прилагается к этой статье.
Ниже приводится доказательство этой формулы.
Доказательство:
Уравнение движения Ньютона, решая которое можно определить координаты и скорости тел в момент времени t, имеет вид:
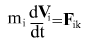
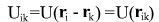 - потенциал зависит от разности координат - потенциал зависит от разности координат
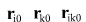 - координаты тел и разности координат в момент времени - координаты тел и разности координат в момент времени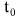
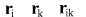 - они же в момент времени - они же в момент времени 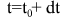
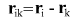
умножая уравнение движения на 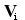 скалярно, получим выражение: скалярно, получим выражение:
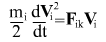
умножив на dt, получаем известное выражение для изменения кинетической энергии тела i, работой 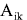 силы силы 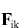 со стороны тела k со стороны тела k
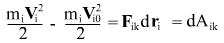
Рассмотрим разность - изменение потенциальной энергии во времени
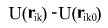
Изменение координат точек за время dt:
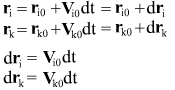
Из двух последних формул следует, что
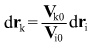 (деление покомпонентное) (деление покомпонентное)
Закон сохранения импульса в системе центра масс имеет вид
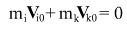
Получаем выражение для отношения скоростей:
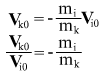
отсюда следует связь между изменениями координат через отношение масс
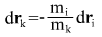
Изменение во времени разности координат:
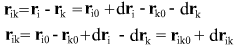
где
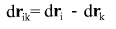
Используя выражение для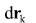 , получим , получим
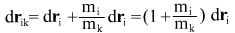
отсюда
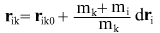
Потенциал в точке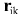 в момент времени, отстоящего на dt от начального, имеет вид: в момент времени, отстоящего на dt от начального, имеет вид:
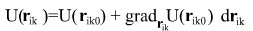
где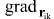 выражается через частные производные по компонентам вектора выражается через частные производные по компонентам вектора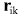
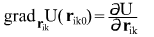
но поскольку по правилу дифференцирования сложной функции
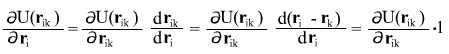
и следовательно
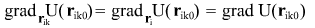
то выражение для потенциала в точке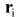 имеет вид имеет вид
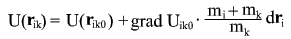
умножим это выражение на
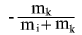
получим
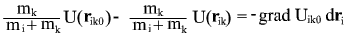
используя выражение для силы через градиент потенциала, получим выражение для работы:
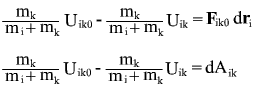
вспомнив, что работа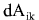 вызывает изменение кинетической энергии, получаем: вызывает изменение кинетической энергии, получаем:
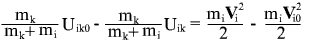
перенося в равенстве величины, относящиеся к одному моменту времени, получим выражение, значение которого не изменилось за временя dt
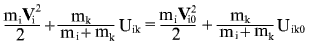
В силу произвольности выбора момента времени 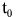 , отсюда следует сохранение во времени значений выражений для двух тел: , отсюда следует сохранение во времени значений выражений для двух тел:
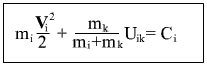
Закон сохранения энергии одного тела как частный случай законов сохранения энергий двух тел или гармоничная вселенная из двух тел.
Если тело k имеет массу много большую, чем тело i, то для тела i формула переходит в известный закон сохранения энергии одного тела в поле консервативных сил:
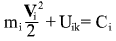
поскольку при больших массах тела k множитель
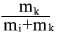
стремится к единице
Но для k-того (тяжелого) тела эта частная формула как закон сохранения энергии совершенно не подходит. В самом деле, из закона сохранения импульса в системе центра масс следует, что скорость k-того тела стремиться к нулю, поскольку из закона сохранения импульса
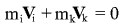
следует, что
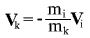
- скорость i-того тела и его масса конечны, поэтому 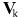 стремится к нулю при увеличении массы. Но из закона сохранения импульса следует, что импульс тела k всегда по модулю в точности равен модулю импульсу тела i, то есть импульс тела k конечен. стремится к нулю при увеличении массы. Но из закона сохранения импульса следует, что импульс тела k всегда по модулю в точности равен модулю импульсу тела i, то есть импульс тела k конечен.
Следовательно значение кинетической энергии тела k пропорционально произведению конечной величины на величину модуля скорости k-того тела, убывающую при росте массы тела k.
Поэтому в формально записанном выражении для "энергии" k-того тела

первым слагаемым в этой формуле следует пренебречь и тогда получим:
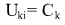
но
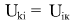
К примеру, в случае кулоновских сил 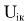 имеет конечные переменные значения, которые меняются обратно пропорционально расстоянию между телами i и к, то есть потециал i-того тела в точке, где находится тяжелое тело k никак не равен нулю и переменен, постольку тело i движется, то есть не константа, хотя с правой стороны стоит именно константа. имеет конечные переменные значения, которые меняются обратно пропорционально расстоянию между телами i и к, то есть потециал i-того тела в точке, где находится тяжелое тело k никак не равен нулю и переменен, постольку тело i движется, то есть не константа, хотя с правой стороны стоит именно константа.
Поэтому для двух тел выражение
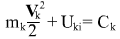
для тяжелого тела абсурдно, хотя имеет смысл для легкого тела, как частный случай для законов сохранения энергии двух тел.
С чисто познавательной точки зрения, закон сохранения энергии одного тела, хотя и дает верные численные значения, но содержит внутреннее противоречие - если тело i меняет движение под действие тела k и при этом сохраняет свою энергию но меняет импульс, то хорошо бы описать как тело i действует на тело k - ведь импульс тяжелого тела меняется так же как импульс легкого.
Но энергия тела k по понятным практическим соображениям, не рассматривалась. Вроде бы оно почти неподвижно и его кинетическая энергия стремится к нулю, но ведь полная энергия включает в себя и потенциал образованный другим телом. То есть возникает чувство потери гармонии в теории.
А вот в законах сохранения энергий двух тел, хотя вся вселенная и очень проста и состоит только из двух тел, но ко всем телам законы сохранения энергии отнеслись с равным уважениям. Даже если одно из них очень тяжелое. Потому что в этом случае оба слагаемых в формуле для энергии тяжелого тела обращаются в ноль
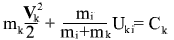
Первое слагаемое, было показно выше, обращается в ноль, а второе слагаемое стремится к нулю, потому что увеличивается знаменатель. То есть общая энергия тяжелого тела, мало того, что константа, она еще стремится к нулю при увеличении массы тяжелого тела.
Вывод: мир из двух тел, при наличии двух законов сохранения энергии, хотя и слишком прост, но гармоничен в описании всех тел.
n-законов сохранения энергии.
Законы сохранения энергии для двух тел имеют познавательную ценность, ровно такую же, как известный закон сохранения энергии для одного тела.
Однако для численного решение задачи многих тел нужно n-законов сохранения энергии. Они нужны для контроля за каждым телом за накоплением ошибок при расчете координат и скоростей при численном интегрировании. Формулы сохранения не связаны с количеством произведенных операций при расчете, но позволяют напрямую вычислить модуль скорости тел без интегрирования, на каждом шаге интегрирования, то есть без накопления ошибок.
Формулы для законов сохранения энергии были первоначально получены мною в результате численного эксперимента.
Благодаря наглядной графике, было замечено, что, значения формул для энергии одного тела в поле консервативных сил, отклоняются от константы, но это отклонение было наглядно связано с массами тел.
Это дало возможность получить верные формулы до их теоретического вывода, проверить их на большом количестве расчетов, после чего появился интерес к теоретическому выводу.
Применение формул для двух тел к системе многих тел, для определенных начальных условий (то начальных положений тел и их скоростей) а также для масс также дало наглядное нарушение "законов сохранение энергий" тел - отклонение от констант.
Оказалось, что полученная формула для двух тел, является частным случаем других более общих законов для n-тел.
Начальные условия были такими:
Было одно, центральное тело, стоящее точно в точке центра масс остальных тел. n-законов сохранения энергии .
Для остальных тел численные эксперименты проводились для трех видом симметрий в начальных условиях:
1) тела одной массы располагались на одном расстоянии от центрального тела, а их начальные скорости закручивались в одну сторону вокруг центрального тела
2) четное количество тел располагалось на одном расстоянии от центрального тела, но скорости четных имели компоненту направленную на нечетные тела, равно как нечетные направлялись к четным с противоположной компонентой скорости.
3) в эксперименте участвовало два тела разных масс, отстоящих от центрального на расстояния обратноропорциональным массам.
Суммарный импульс во всех случаях был равен нулю.
Вклады от потенциалов в формулах для энергии расчитывались по формулам для двух тел если тело находилось в окружении центрального тела, а вот вклад потенциала центрального тела отличался.
Вклад от потенциалов окружающих тел в точке нахождения центрального тела был равен нулю, а вклад потенциала центрального тела в формулы для расчета энергии окружающих его тел не зависел от масс - то есть умножался на 1.
При этом формулы для расчета энергии давали константы для всех тел, то есть, чем точнее делался расчет траекторий тел, тем меньше менялась энергия, расчитанная по модифицированным формулам.
Очевидно, что есть более широкий класс формул, которые дает возможность рассчитывать сохраняющиеся энергии тел, в которых коэффициенты перед вкладом потенциалов меняются так, сумма коэффициентов перед взаимодействующими потенциалами равна единице, но есть ли при этом возможность получить общие формулы? Однако, надежда на существование таких формул сохраняется.
Результаты расчетов для многих тел "как они есть" прилагаются к программе, которая тестирует два закона сохранения. Для тех, кому возможность открыть новые n интегралов, в дополнении к 10 существующим в классической механике, кажется увлекательной, эти расчеты, возможно, дадут импульс к новым идеям для вывода законов сохранения.
Попытайтесь их получить и Вы, возможно, войдете в учебники физики.
Тестирующая программа.
Цель программы показать, что на траекториях, являющихся решением уравнения Ньютона для двух тел законы сохранения выполняются точно, а если траектории отклоняются от точного решения, то в точках траектории значения энергий, рассчитанных по предлагаемой формуле, отклоняются от начальных.
Вы можете приобрести программу (через PayPal), которая наглядно производит численные расчеты траекторий двух тел для трех видов потенциалов взаимодействия двух тел:
1) закон Кулона, потенциал которого обратно пропорционален расстоянию между телами.
2) заряженные сферы вокруг тел, заданного радиуса, внутри которых, как известно, силы взаимодействия между телами равны нулю и тела движутся по прямой до столкновения с границами сферы, а при расстоянии между телами больше радиуса сферы, потенциал заряженных тел совпадает с кулоновским потенциалом.
3) упругие силы, которые возрастают при увеличении расстояния между телами, потенциал упругих сил пропорционален квадрату расстояния между телами.
Средства от продажи предназначаются для разработки программно-аппаратных средств ранней диагностики заболеваний в домашних условий. Зайдите на мой сайт vv-voronkov.spb.ru и Вы убедитесь, что автор активно работает в этой области. Причем мои результаты реально уже много лет работают для диагностики заболеваний на гамма-камерах. То есть мне можно верить. Поэтому проникнетесь состраданием к людям и внесите свой вклад на общие цели.
Оплачивая программу Вы можете помочь самому себе.
Численная схема выбиралась из соображения максимальной простоты - она понятна даже продвинутым школьникам средних школ, покольку она исходит из предположения, что при уменьшении шага итегрирования по времени dt, сила на отрезке меняется мало, и тогда можно применять формулы для движения тела в постоянных силах. На шаге интегрирования dt на отрезке от начального момента времени 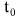 до до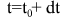 , изменение координат и скоростей рассчитывается по формулам : , изменение координат и скоростей рассчитывается по формулам :
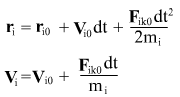
здесь и далее dt уже не бесконечная малая величина, а конечное число, которое можно легко менять в программе кликом мыши по шкале dt (справа).
Эта численная схема дает показательно большую погрешность, но для тестирования законов сохранения это достоинство, поскольку цель программы показывать реакцию законов на оклонение от точных, истинных траекторий. Но в практических задачах, конечно, нужно выбирать значительно лучшие схемы.
Нажимая на клавиши V и R и перемещая мышь, можно менять скорость и координату тела i=1, координата и скорость тела k=2 переcчитывается по формулам:
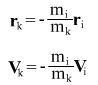
Фиксация скорости и координаты выполняется при нажатии на клавиши клавиатуры или мыши.
Массы и заряды тел меняются кликом левой клавиши мыши по соответсвующим шкалам, равно как длительность интервала интегрирования по времени 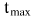
При первом запуске программы выполняется серия демонстрационных расчетов, которые доказывают, что энергии 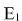 и и 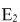 для каждой точки траекторий приближаются к константе - своим начальным значениям в момент времени t=0 тем сильнее, чем меньше dt - то есть чем расчетная траектория ближе к истинной траектории. для каждой точки траекторий приближаются к константе - своим начальным значениям в момент времени t=0 тем сильнее, чем меньше dt - то есть чем расчетная траектория ближе к истинной траектории.
Для этого на экране строятся два графика разностей 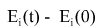 , которые при dt стремящемся к нулю превращаются в прямые линии, что говорит о сохранности энергий тел, рассчитанных по предлагаемой формуле, которая приведена здесь и выводится программой на экран. , которые при dt стремящемся к нулю превращаются в прямые линии, что говорит о сохранности энергий тел, рассчитанных по предлагаемой формуле, которая приведена здесь и выводится программой на экран.
Масштаб вывода графиков меняется с помощью соответствующей шкалы.
Числовые значения энергий выводятся в нескольких точках на графиках разностей энергий и сводятся в таблицы.
Чтобы облегчить сравнение чисел, в таблицах подчеркиваются десятичные знаки значений энергии, совпадающие с десятичными знаками энергий в начальный момент времени.
Так же строятся две диаграммы совпадений десятичных знаков и рассчитывается среднее количество совпавших десятичных знаков, которое выводится под диаграммой.
Нужно иметь ввиду, что добавление одного десятичного знака означает увеличения точности сохранения энергий в десять раз.
Программа выводит конечные результаты расчетов при демонстрации в файлы в формате jpg, которые она демонстрирует как мультики, с тем, чтобы облегчить наблюдение над сходимостью энергий к константе.
Просматривать эти файлы также можно прокручивая колесико мыши.
Повторять демострационные расчеты можно нажимая на клавиши D или T, а кликом на правую клавишу мыши можно делать расчет для заданного набора параметров.
Сохранять результаты расчетов в файлах в формате jpg можно нажимая на клавишу J.
Нажатием клавиши P, Вы можете получить тексты программ на языке C++ для заданного набора параметров, в которых Вы можете увидеть все формулы для расчетов, упомянутые в этой статье.
Построив и запустив программу, Вы получите файл с результатами расчетов и сможете с помощью MatLab убедиться в истинности двух законов сохранения энергий.
Автор выражает благодарность Михаилу Соколову, Олегу Воронкову и Владимиру Бессонову, оказавшим мне техническую помощь в подготовке этого сайта. |