Two new Laws of Conservation of Energy for Two-body Problem. The results of numerical calculations for n-Laws of Conservation of Energy for n-body
Victor Voronkov. vv-2000@list.ru September-November 2013
See film.
It is considered that for the system of bodies interacting by means of conservative forces, there is only one law of conservation of total (full) energy of all bodies.
However for the general knowledge and likewise for practical purposes of numerical integration of system of the equations of motion, of great interest are the laws of conservation of energy for each of the interacting bodies. In the latter case the existence of a formula which will allow to check calculation error for each body in a problem of many bodies, irrespective of the number of integration steps and the chosen numerical method, is of great value.
Therefore I show below the derivation of two laws of conservation of energy in a problem of two bodies and give results of calculation for many bodies which show that the existence of n of conservation laws of energy for the system of n-bodies is possible.
Laws of Conservation of Energy for each body in the problem of two bodies in system of coordinates of the center of masses are given by:
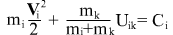
here i and k ‚Äď body numbers: i=1,2 k=2,1
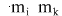 - mass of bodies - mass of bodies
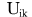 - potential of body k in location of body i - potential of body k in location of body i
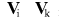 - velocity of i and k bodies in t time point - velocity of i and k bodies in t time point
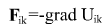 - The conservative force acting on body i from body k - The conservative force acting on body i from body k
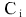 - constant (time-independent value) - constant (time-independent value)
You can test the formula for conservation of energy by means of the TWO-LAW Program which is attached to this article
Proof of this formula is given below.
Proof:
Newton's equation of motion, in solving which it is possible to determine coordinates and velocities of bodies in t time point, is given by:
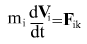
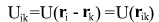 - potential depends on the difference of coordinates - potential depends on the difference of coordinates
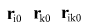 - coordinates of bodies and differences of coordinates at time point - coordinates of bodies and differences of coordinates at time point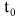
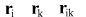 - same at time point - same at time point 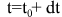
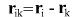
Scalarly multiply the motion equation by 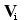 to obtain: to obtain:
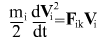
multiply by dt to obtain the known expression for the change of kinetic energy of body i by work 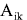 of force of force 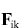 from body k from body k
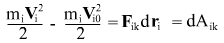
Consider difference ‚Äď change of potential energy over time
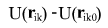
Change in point positions in time dt:
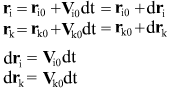
It follows from the two last formulas that
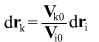 (componentwise division) (componentwise division)
Law of conservation of momentum in the center-of-mass system is given by
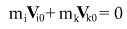
Obtain expression for velocity ratio:
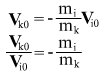
hence follows the relation between change of coordinates in terms of mass ratio
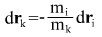
Change of difference of coordinates in time:
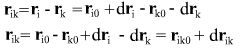
where
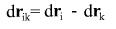
Use expression for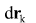 to obtain to obtain
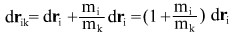
hence follows
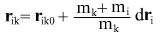
Potential at point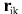 at the instant of time which is at dt interval from the initial time point is given by: at the instant of time which is at dt interval from the initial time point is given by:
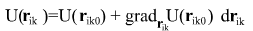
where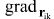 is expressed in terms of partial derivatives with respect to components of vector is expressed in terms of partial derivatives with respect to components of vector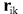
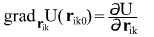
considering however that under the chain rule
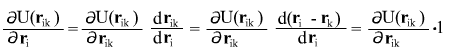
and hence
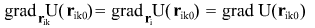
it follows that the expression for potential at point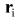 is given by is given by
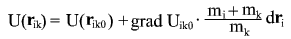
multiply this expression by
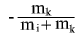
to obtain
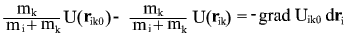
use expression for force in terms of potential gradient to obtain expression for work:
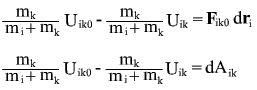
remembering that work causes the change of kinetic energy, it follows that: causes the change of kinetic energy, it follows that:
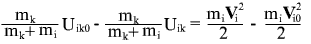
by interchanging the values referring to the same instant of time, we obtain the expression which value has not changed in time dt
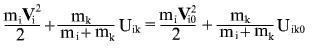
Due to the arbitrary choice of instant 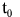 , hence follows invariable (in time) values of expressions for two bodies: , hence follows invariable (in time) values of expressions for two bodies:
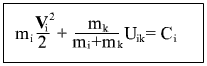
One-body Law of Conservation of Energy as specific case of Laws of Conservation of Energy OR consistent two-body universe.
If the mass of body k is much bigger than that of body i, then the formula for body i will go into the known One-body Law of Conservation of Energy in the field of conservative forces:
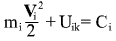
considering that with big masses of body k the factor
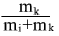
tends to one
However for k-th (heavy) body this specific formula is absolutely not applicable. In fact it follows from the law of conservation of momentum in center-of-mass system, that velocity of k-th body tends to zero, because it follows from the law of conservation of momentum
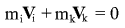
that
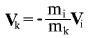
- velocity of i-th body and its mass are finite, therefore 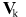 tends to zero when the mass increases. However it follows from the law of conservation of momentum that momentum of body k is always exactly equal to momentum modulus of body i, i.e. momentum of body k is finite. tends to zero when the mass increases. However it follows from the law of conservation of momentum that momentum of body k is always exactly equal to momentum modulus of body i, i.e. momentum of body k is finite.
Therefore kinetic energy of body k is in proportion to the product of finite value and the velocity modulus of k-th body, decreasing with the increase of mass of body k.
Therefore in the formal expression for "enrrgy" of k-th body
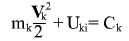
the first summand in this formula should be neglected; hence we obtain:
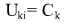
but
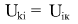
For example in the case of Coulomb forces 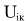 has finite variable values, that are changing in inverse proportion to the distance between bodies i and k, i.e. potential of i-th body in the location of the heavy body k is in no case zero and is running, because body i is moving. i.e. potential is not a constant, though it is a constant on the right side. has finite variable values, that are changing in inverse proportion to the distance between bodies i and k, i.e. potential of i-th body in the location of the heavy body k is in no case zero and is running, because body i is moving. i.e. potential is not a constant, though it is a constant on the right side.
Hence for two bodies the following expression
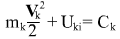
is absurd for the heavy body, although it is meaningful for the light body, as specific case of Two-body Laws of Conservation of Energy.
For purely cognitive purposes One-body Law of Conservation of Energy ‚Äď although giving correct numerical values, contains inherent contradiction: if body i changes motion due to the action of body k, and while conserving its energy it changes its momentum, it is worthwhile to describe how body i affects body k ‚Äď considering that momentum of the heavy body changes in the same way as does momentum of the light body.
However energy of body k was never considered for understandable practical reasons. It is seemingly nearly motionless and its kinetic energy tends to zero, but it should be noted that total energy includes also potential made by another body. That is to say the consistency of the theory seems to wane.
Whereas in the Two-body Laws of Conservation of Energy, though the universe is essentially made only of two bodies and hence is very simple, yet Laws of Conservation of Energy have treated all bodies equally with respect. Even though one of them is very heavy. Because in this case both summands in the formula for the heavy body become zero.
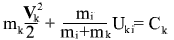
First summand, as was shown above, becomes zero, and addend tends to zero, because the denominator increases. That is total energy of the heavy body not is only a constant, but it also tends to zero at the increase of the mass of this heavy body.
Conclusion: with the two Laws of Conservation of Energy the two-body world, though being very simple ‚Äď is truly consistent in the description of all bodies.
n-Laws of Conservation of Energy.
Two-body Laws of Conservation of Energy have cognitive value in the same way as does the well-known One-body Law of Conservation of Energy.
However for the numeric solution of many-body problem it is necessary to have n-Laws of Conservation of Energy. They are needed to control each body, i.e. to check accumulation of errors at calculation of coordinates and velocities in numerical integration. Conservation formulas do not depend on the number of calculation operations, but they enable to directly calculate the velocity modulus of bodies without integration, at each integration step, i.e. with no accumulated errors.
My formulas for Laws of Conservation of Energy were first developed in the numerical experiment.
Visual graphic helped to see that values in the formulas for the energy of one body in the field of conservative forces deviated from the constant, but this deviation was clearly related to the masses of the bodies.
This enabled to develop correct formulas before they have been derived, and to test them in a large number of calculations. This in turn encouraged to do the derivation.
Application of two-body formulas to many-body system, with certain starting conditions (i.e. initial position of bodies and their velocities), and for masses has also clearly proven deviance of the "Laws of Conservation of Energy" for bodies, i.e. deviation from constants.
It appeared that the developed two-body formula was a specific case of other, more general n-body laws.
Starting conditions were as follows:
There was one central body located exactly in the centre point of mass of the other bodies.
For the other bodies numerical experiments were made for the three types of symmetry with the following starting conditions:
1) bodies of the same mass were at the same distance from the central body with their initial velocities spinning in the same direction around the central body
2) even number of bodies were located at the same distance from the central body, but the velocities of the even bodies were having a component directed on the odd bodies, in the same way as the odd bodies were directed to the even ones with the opposite velocity component.
3) two bodies with different mass were used in the experiment, both apart from the central body at a distance inversely proportional to their masses.
Total momentum in all cases was zero.
Contributions by the potentials in formulas for energy were calculated by formulas for two bodies if the body was in the environment of the central body, whereas the contribution by the potential of the central body was different
Deposits in formulas for energy calculated from potentials on formulas for two bodies if the body was in an environment of the central body, but the contribution of potential of the central body differed.
Contribution by the potentials of the surrounding bodies at the location of the central body was zero, whereas contribution by the potential of the central body to the energy calculation formulas for its surrounding bodies did not depend on the masses ‚Äď i.e. was multiplied by 1.
In this case energy calculation formulas were giving constants for all bodies, i.e. the more accurate was the calculation of bodies’ trajectories, the less was the change of energy, calculated with the use of modified formulas.
There is obviously wider class of formulas that allow calculation of conserved energies of bodies, in which coefficients before contribution by the potentials are changing in such a way that the sum of coefficients before interacting potentials amounts to one, but is there a way to develop any generalized formulas? Yet there is a hope that such formulas may exist.
Calculation data for many bodies "as they are" are attached to the Program for testing two Laws of Conservation of Energy. For those readers who may get engrossed with discovering new n integrals in addition to those 10 existing in classical mechanics, these calculations may come as a challenge for developing their laws of conservation.
It may be your turn to make a try and write your name in physics.
Testing Program.
Main objective of the Program is to show that for the trajectories that are received in the solution of the two-body Newton’s equation, Laws of Conservation of Energy are accurately applicative, whereas if the trajectories deviate from the accurate solution, then in the points of trajectories the energy values as calculated by the suggested formula, deviate from the original energy values.
You may buy the Program(through PayPal), which offers graphic numerical calculations of trajectories of two bodies for three types of two-body interaction potential:
1) Coulomb Law, where the potential is reversely proportional to the distance between the bodies.
2) charged spheres of the known radius around the bodies, where, as is known, forces of body interaction amount to zero and bodies move in a straight line until collision with the sphere boundaries, whereas if the distance between the bodies is exceeding radius of the sphere, the potential of the charged bodies is calculated by the formula for Coulomb potential.
3) elastic forces, increasing at the increase of distance between the bodies, potential of the elastic forces is proportional to the squared distance between the bodies.
Receipts from the sale of the Application will be used for the development of soft hardware for early at-home disease detection. For more information visit the author’s site at www.vv-voronkov.spb.ru to get the idea of my efforts in this field. My accomplishments have been long used in the disease detection with gamma-cameras. It stands for my good faith. This may open you the way to compassion and lofty aids.
Your payment for the Application may help you to help yourself.
The choice of numerical method was based on consideration of simplicity ‚Äď it may be easily understood even by some advanced school students, as it proceeds from the assumption that with the decrease of integration step over time dt the force in the interval will change insignificantly, which means it is possible to use the formula for the body motion in constant forces. With integration step dt at the interval from the initial instant of time 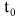 to to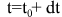 , change of coordinates and velocities may be calculated by the following formulas: , change of coordinates and velocities may be calculated by the following formulas:
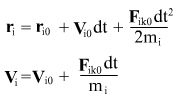
In what follows dt is no more an infinitesimal, but rather a finite number, which can be easily changed in the Program by clicking on scale dt (on the right).
This calculation method gives significantly low accuracy, but it is an advantage for testing laws of conservation, as the objective of the Program is to demonstrate how the laws respond to deviation from accurate true trajectories. For practical purposes it is obviously necessary to choose much better algorithms.
By pressing V and R keys and dragging a mouse you can change velocity value and coordinate of body i=1; coordinate and velocity of body k=2 may be recalculated by the following formulas:
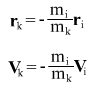
Velocity and coordinates may be fixed from the keyboard or with a mouse.
Body masses and charges may be changed by left click on corresponding scales, in the same way as the length of integration interval 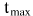
At the first run the Program will start a set of demo calculations which prove that energies 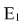 –ł –ł 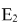 for each point of trajectory verge to a constant ‚Äď i.e. their initial values at instant t=0 ‚Äď the more so the less is dt ‚Äď i.e. the closer the calculated trajectory to the actual trajectory. for each point of trajectory verge to a constant ‚Äď i.e. their initial values at instant t=0 ‚Äď the more so the less is dt ‚Äď i.e. the closer the calculated trajectory to the actual trajectory.
For this purpose the display shows the plotting of the graph of differences 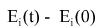 , which with dt tending to zero, become straight lines, which proves conservation of body energies, as calculated with the above formula, and is displayed in the Program. , which with dt tending to zero, become straight lines, which proves conservation of body energies, as calculated with the above formula, and is displayed in the Program.
The graphs may be zoomed by using corresponding scales.
Numerical values of the energies are displayed at several points on the graphs of energy differences and are tabulated.
For the ease and convenience of comparison, decimal digits in the energy values that coincide with the energy decimals at the initial instant are underlined in the tables.
Also two diagrams are made for decimal coincidence with calculation of the average number of such coincidences which is displayed at the bottom of the diagram.
It should be noted that one decimal increment means tenfold increase of the energy conservation accuracy.
On demo run final calculation data are output in jpg files and are displayed as animated cartoons in order to facilitate observation of convergence of energies to constant.
These files may be also viewed with mouse wheel.
Demo calculations may be repeatedly done by pressing D or T keys; and by right click it is possible to make calculations for the pre-chosen set of values.
Calculation data may be saved in jpg files by pressing J key.
By pressing P key you may have source codes in –°++ for the pre-chosen set of values, where you can see all calculation formulas referred to in this article.
When you build and run the Application you will have a file with calculation data and use MatLab to ascertain the verity of the two Laws of Conservation of Energy.
.
The author expresses thanks to Mikhail Sokolov, Oleg Voronkov and Vladimir Bessonov for their technical support in the development of this website. |